Let us try to view some of these issues in a semi-classical way, and as was described in the companion document The Golf Ball Problem, let us assume that a subatomic particle, say, a proton, can be approximated by a miscible sphere with a finite radius, $R$ and a density, $\rho_0$ which is constant throughout the volume of the sphere. The equations for the potential, $V$ and the force, $F$ are as follows:
The force on the golf ball when it is at $R$: $$ F = (4/3) k m \pi \rho_0 \, R$$ The potential at $R$: $$ V = - (2/3) k m \pi \rho_0 \, R^2$$
The force on the golf ball at $r$, where $r$ < $R$ is $$ F = (4/3) k m \pi \rho_0 \, r $$ The potential at r: $$ V = - (2/3) k m \pi \rho_0 \, r^2 $$
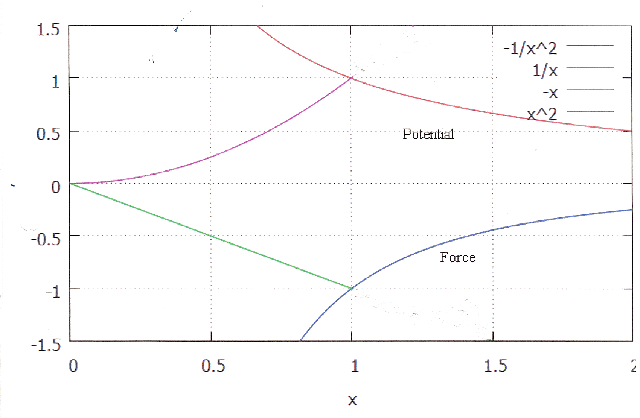
A plot of the potential function, $V$, and the force, $F$ is shown in the figure immediately below. The ordinate, $y$, is a measure of the force, $F$, and the potential, $V$. The abscissa,$x$, is the value of $r$.
The plots are scaled so that when $y = 1$, the value of $F$ is $(4/3) k m \pi \rho_0 $ and when $y = 1$ the value of the potential, $V$ is $- (2/3) k m \pi \rho_0$. Also, the plots are scaled so that when $x = 1$, the value of $r$ is $R$, the outer surface of the sphere.

If we follow the two plots from right to left, we see the values of the Newtonian force and potential. At $r=R$ (i.e., when $x=1$), the plots bifurcate with one branch following the path to infinity, as would be predicted by Newton. However, the second branch follows quite a different path. The force goes to $0$ in a linear manner as $x$ approaches $0$, as shown in the above equation. The potential follows the path shown by the equation, above. If one views a three dimensional plot of the potential, a shape is shown that is similar to a sombrero.
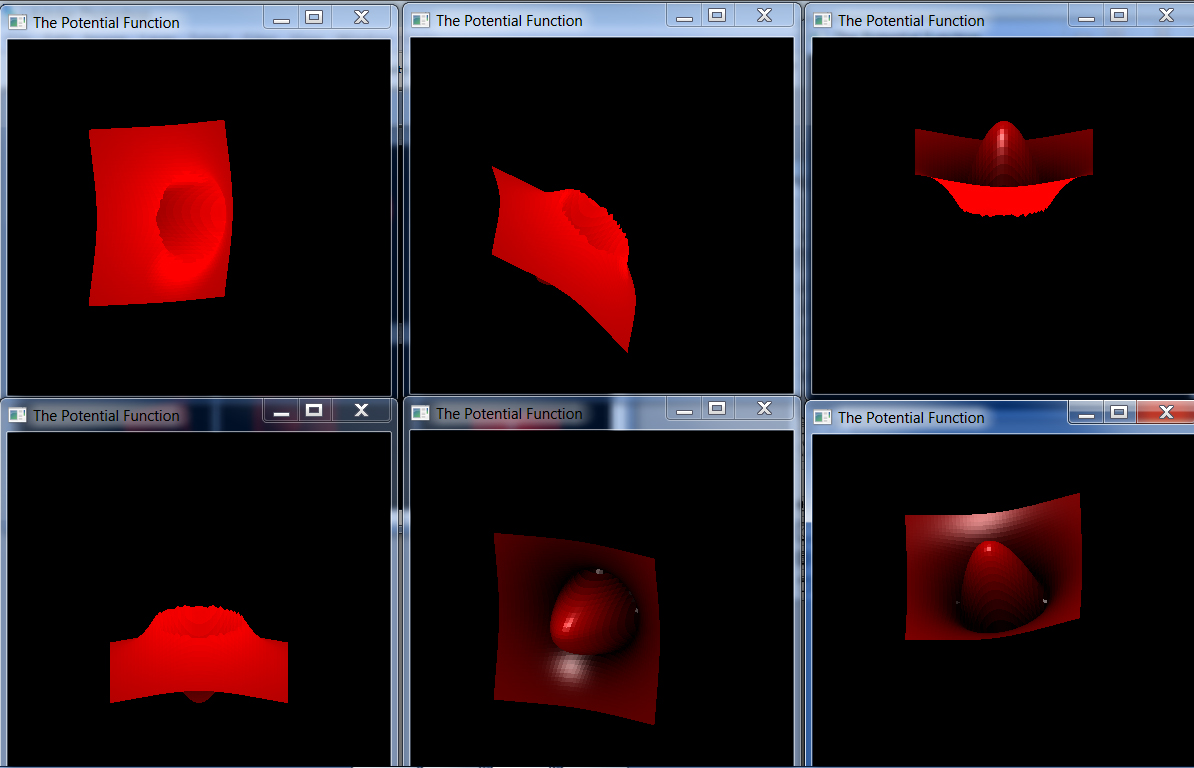
At sub-atomic distances, the "Mexican Hat" shape of the potential function avoids the infinities that have been encountered in calculations that employed functions that contained singularities.
Let us say that, by some special mechanism, the total energy of a particle is less that the peak found in the potential function at $r = R$. If the second particle were to be found with $r$ less than $R$, the particle would be bound to the second particle, yet the kinetic energy would not be $0$. Instead, the second particle would rattle back in forth in that potential well.
At subatomic distances this zitterbewegung (Gr. zitter=shake, bewegung=motion) allows calculations to show how bindings of two or more particles is possible, and energetically advantageous. This situation allows the moieties of mass, charge, and spin to 'clump', but only to a very limited extent. The attraction of one moiety type that is experienced by another type is seen only at extremely short distances. So, a single proton, one or two neutrons, maybe an electron, neutrino, etc. will clump. But further clumping does not occur because the additional particles can not get physically close enough to feel this short range force. In nature a set of protons will clump with (roughly) the same number of neutrons, only.
The mechanism of dropping the energy of a particle into this potential hole is not presented here. This was the dream of the alchemists; they had no explanations, either.